资本资产定价模型(CAPM) - 结合国家风险溢价的股票风险溢价(ERP)#

pic

Fig. 8 结合国家风险溢价的股票风险溢价(ERP)#

前言#

正如我在资本资产定价模型(CAPM) - 历史数据得出的股票风险溢价(ERP)的利弊 里面所介绍，用大盘的历史数据来求股票风险溢价 (Equity Risk Premium)存在着各种弊端和考量的事情。并不是说这种方法不好，但用的时候要权衡利弊。本文将继续承接股票风险溢价的话题，不过今次将用另类的角度来求股票风险溢价 (Equity Risk Premium)。

预期回报率(Expected Return)公式

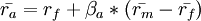
formula

Fig. 9 单个股票或者股票组合的预期回报率(Expected Return)公式#

股票风险溢价 (Equity Risk Premium)#

这样说吧，中国从1800年至今都没有发生过任何国债违约事件资本资产定价模型(CAPM) - 无风险收益率（rf）的探讨和使用， 但我们始终是发展中国家，所以按照资本市场的定义，我们国家发行的国债还是存在的一定风险的。那谁发的国债就没有风险啊？

嗯，就是这样一回事。现今还是美国说了算，如果他家的国债都违约了，那就“七国咁乱”了。 所以我们可以假设美国是没有违约风险的，那国家风险溢价（country risk premium）自自然然也为零。我们首先以美国的隐含股票风险溢价(implied equity risk premium)作为基础，再叠加国家风险溢价（country risk premium），最终就可以通过发达国家（如美国）的ERP叠加得到发展中国家的股票风险溢价 (Equity Risk Premium)。公式大致是这样的：

ERP（中国） = 隐含股票风险溢价（美国） + 国家风险溢价（中国）

1. 隐含股票风险溢价(implied equity risk premium)#

隐含股票风险溢价的计算方法较为复杂，主要是利用了现金流贴现模型（DCF Model）来实现，并作出相应的数据假设。

  1. 首先计算S&P500指数过往5年的分红、回购得到平均占比（%）；

  2. 获得最新S&P500指数数据后，乘以上述的平均占比（%），得到预期的分红、回购数值；

  3. 至于DCF中的增长率（g）就要通过各大权威分析师给出的预测值获得；然后通过增长率（g）乘以预期的分红、回购数值计算未来5年的现金流；

  4. 最后求得未知数 r (implied equity risk premium)。

具体例子

formula

Fig. 10 Credits: Aswath Damodaran，Implied Equity Premiums: January 2008#

2. 国家风险溢价（country risk premium）#

这里所说的违约风险主要通过穆迪评级（Moody’s Rating）或者信用违约互换(credit default swap, CDS)转换得到。 但这里要注意的是因为股票的风险和债券的风险不一样，所以我们需要用股票的标准差除以债券的标准差，再乘以穆迪评级的利差或者CDS才算是比较准确的得到国家风险溢价（country risk premium）。

如美国的穆迪评级（Moody’s Rating）为最高级Aaa， 那么它所对应的利差为0； 中国的穆迪评级（Moody’s Rating）为A1，那么中国所对应的利差为0.79%。 假设美国的2019年1月的Implied ERP为5.96，股票和债券标准差自己的乘数为1.23， 中国所对应的利差为0.79%，那么， ERP（中国） = 5.96% + 1.23*0.79% = 6.94%

如美国的主权信用违约互换（Sovereign CDS）为0； 中国的主权信用违约互换（Sovereign CDS）为0.84%。那么， ERP（中国） = 5.96% + 1.23*0.84% = 6.99%

结尾#

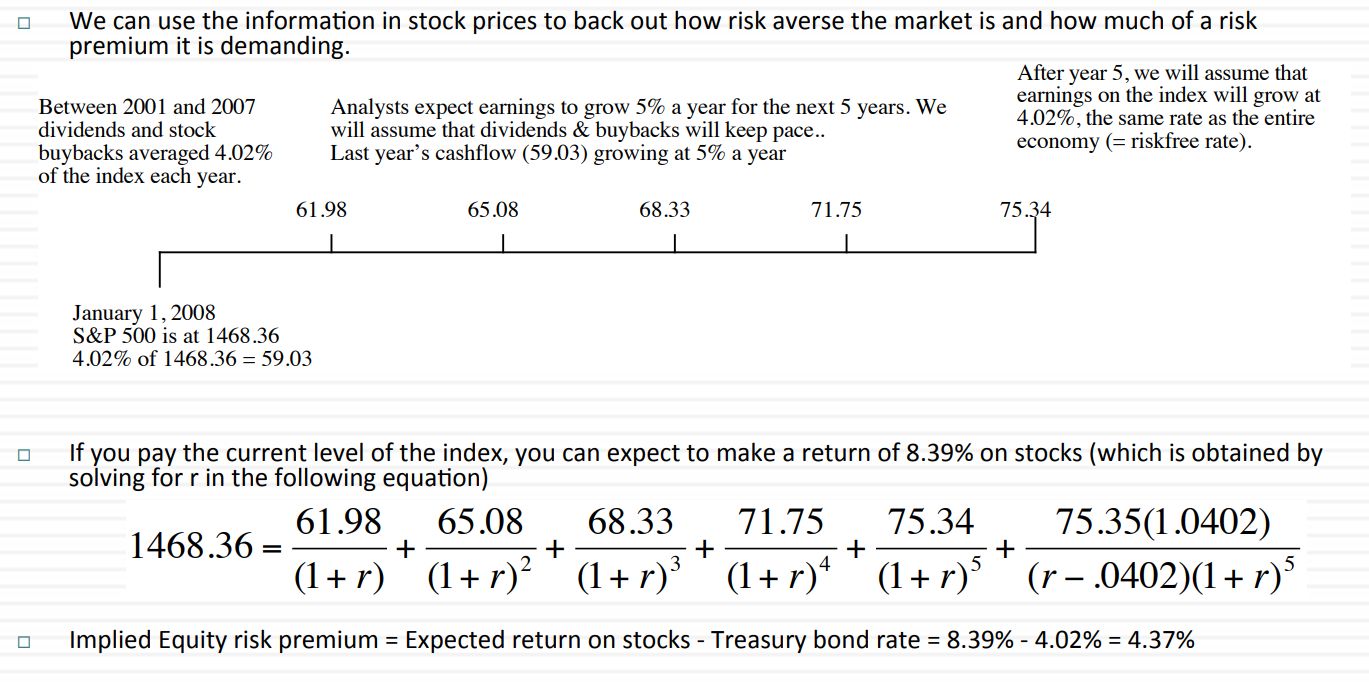
以上的数据可以通过Bloomberg Terminal 得到。之前一直google或者baidu寻找免费的数据来源来验证上面的计算方法，可惜找了好几天都是无果。 真的没有办法，归根结底还是太穷了，买不起Bloomberg Terminal 。如果有人能提供免费数据的话，可以测试一下。

不过没有数据也不要紧，我尊敬的Aswath Damodaran已经帮我们全部计算好，并提供了下载。他的数据是直接从Bloomberg Terminal 下载的，不用质疑。

参考数据：股票风险溢价(ERP)

下载：excel