对数转换（Log Transformation） 和 标准化(z-score) 的区别#

一、不同点#

（1）数据标准化（z-score/Standard Scaler）#

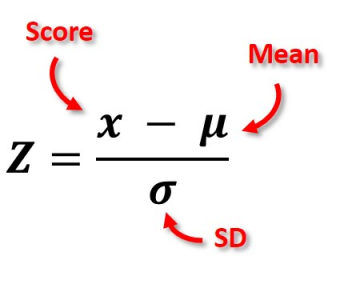
Z-Score

Fig. 30 Source: simplypsychology.org#

Tip

数据标准化（z-score）不会改变分布(distribution)的偏斜（skewness）。它只是原始数据的均值(mean)和方差(variance)分别转为 0 和 1 ，即 μ=0 和 σ2=1。 但实际的分布形状是保持不变的。

需要注意的是，标准化后没有改变分布形状（改变偏度）的原因在于， 数据集中的异常值会影响用于缩放要素的均值和标准差。

（2）Log-transformation#

Tip

对数转换（Log-transformation）会改变分布(distribution)的偏斜（skewness），并处理具有右尾分布（right-tailed distribution）的值。

值得注意的是， ‎对数转换（Log-transformation）的缺陷在于它仅适用于非零和非负数据，并且不会转换为预定的尺度， 即转换后的数值始终是介于 [0-1] 之间。‎

对于金融相关的具有时间序列的数据，正如大佬 David Ruppert & David S. Matteson 在《Statistics and Data Analysis for Financial Engineering, Second Edition》书上提及过，应该用对数转换（Log-transformation）来处理数据，因为这样处理后的数据更具平稳性，更适用于做回归分析。

As mentioned, many financial time series do not exhibit stationarity, but often the changes in them, perhaps after applying a log transformation, are approximately stationary.

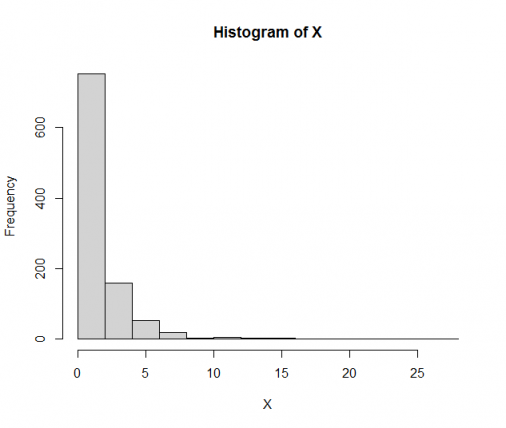
二、偏斜的分布（长右尾）图#

如下图所示， 这是一个随机生成具有偏斜的分布（长右尾）的 图X：

set.seed(0)
X <- rlnorm(1000)
hist(X)

现在我们执行两个转换，如下所示：

  1. Z, 数据标准化（z-score）

  2. L, 对数转换（Log-transformation）

Z <- (X-mean(X))/sd(X)
L <- log(X)
par(mfrow = c(1,2))
hist(Z)
hist(L)

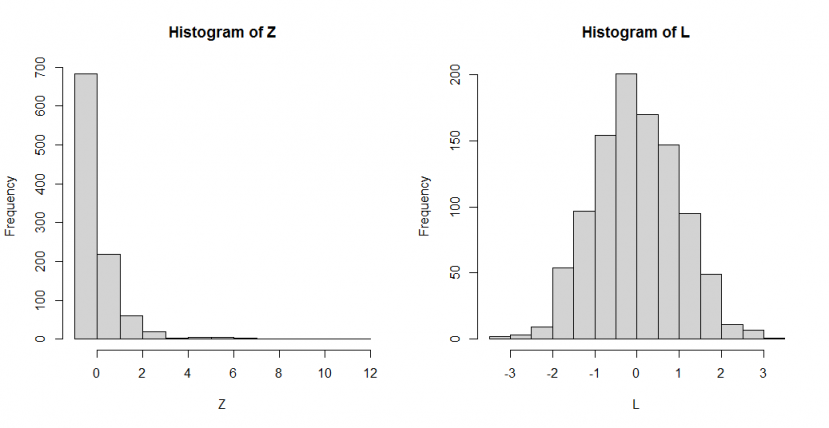
如上图所示，

  • 数据标准化（z-score）后（图Z）与 图X 具有相似的形状分布， 但其均值(mean)和方差(variance)已分别转为 0 和 1， 但这并不改变分布(distribution)原来的偏斜（skewness）；

  • 数据对数转换后（图L）已经消除了长右尾，图形已呈现正态分布。

三、指数分布图#

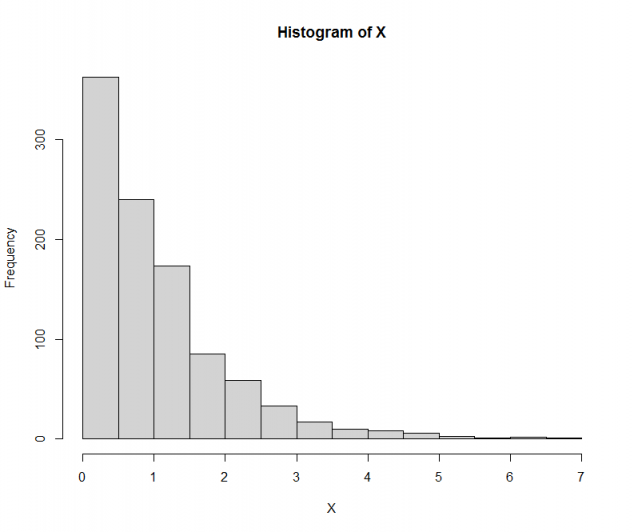
值得注意的是，如果数据集 X 是呈指数分布的，则对数转换后的变量可能不是正态变量，如下图所示（指数分布）：

set.seed(0)
X <- rexp(1000)
par(mfrow = c(1,1))
hist(X)


Z <- (X-mean(X))/sd(X)
L <- log(X)
par(mfrow = c(1,2))
hist(Z)
hist(L)

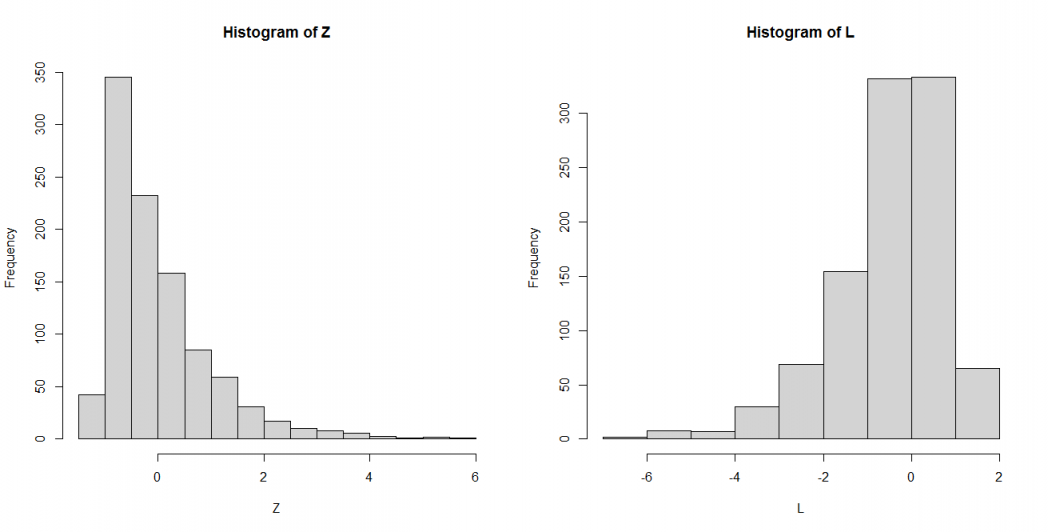
你可以看到，对数转换的 数据集X（图L）的分布现在没有了右尾，但看起来也不是正态分布，因为它仍然是偏斜的。所以说，对数转换这个方法并不总是使变量呈正态分布。

四、总结#

（1）Log Transformer#

  • Helps with skewness

  • No predetermined range for scaled data

  • Useful only on non-zero, non-negative data

  • Best for time-series data

（2）Standard Scaler#

  • Shifts distribution’s mean to 0 & unit variance

  • No predetermined range

  • Best to use on data that is approximately normally distributed

其实经过两者对比之后，我发现之前研究 线性回归(LR) 中的例子可能有几个地方作者在数据处理方面不是很恰当。

参考#