Factor Analysis - 因子分析#

Factor Analysis

Factor Analysis tries to find latent variables1 that make sense to us. We can rotate the solution until we find latent variables that have a clear interpretation and “make sense”.

– Joos Korstanje

一、目的#

因子分析（Factor Analysis）目的在于在众多的数据特征中找出影响数据集最高的几个特征，或者理解为将多个变量压缩归集为新的特征变量，从而更好地解释、理解数据集。

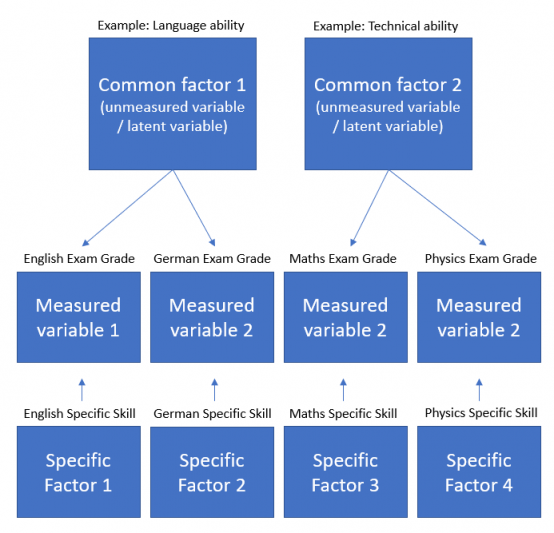
Schematic example of Common Factor Model

Fig. 23 Schematic example of Common Factor Model By Joos Korstanje.#

上面这个从大佬JK那里照搬的架构图可以很好地说明子分析：

  • 假设一所高中学校里有很多学生

  • 每个学生拥有多个科目（Measured variable）的的成绩单（如生物、化学、物理，历史、政治、地理，语文、英文等）

  • 假设这些不同的成绩是部分相关的

Tip

1、假如某一个学生的生物、化学、物理、数学成绩是特别6的，那么老师会认为这个学生的理科特别好，那么这个学生会被分配到理科班；

2、假如某一个学生的历史、政治、地理，语文成绩是特别6的，那么老师会认为这个学生的文科特别好，那么这个学生会被分配到文科班；

下面是从DataCamp找到的另外一个架构图，用于更好理解FA：

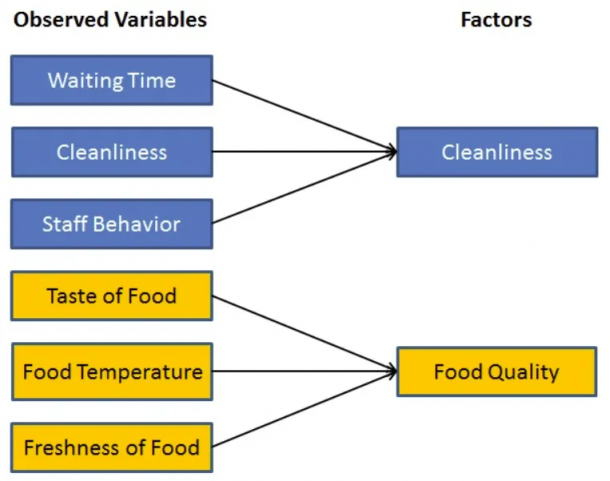
DataCamp

Fig. 24 Source: DataCamp.#

Tip

如图所展示的，“食物的味道、食物的温度、食物的新鲜度”这三个变量（特征）通过因子分析（Factor Analysis）可以压缩归集出一个新变量（所谓的隐性变量，latent variables），食物的品质， 去概括前面所述的是三个特征。

二、原理#

‎因子分析（Factor Analysis）基于公共因子模型(common factor model)。原则：数据集中存在一定数量的因子，并且每个测量的变量都捕获了一个或多个这些因子的一部分。‎

‎如前所述，因子分析中的数学模型比PCA模型更具概念性。PCA模型更像是一种务实的方法，在因子分析中，我们假设存在潜在变量（latent variables）。‎

三、何时使用PCA or FA#

1、Principal Component Analysis - 主成分分析#

  • 数据集中的指标（变量）数量过多，不便于数据分析

  • 假设数据集中没有任何测量误差或噪声noise

2、Factor Analysis - 因子分析#

  • 对数据集的变量降维（减少变量）没有兴趣

  • 希望找出数据集中某些最具解释力度的变量

  • 例如，在心理学中：将很长的个性测试反馈减少为只有少量的个性特质

  • 例如，在市场营销中：将包含了各种各样问题的产品评估问卷调查归类为几个因子，用于产品改进

四、Python实现方式#

from sklearn.decomposition import FactorAnalysis
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
my_fa = FactorAnalysis(n_components=2)
# in new version of sklearn:
# my_fa = FactorAnalysis(n_components=2, rotation='varimax')
X_transformed = my_fa.fit_transform(X)

参考：

  1. What is the difference between PCA and Factor Analysis? | by Joos Korstanje | Towards Data Science

  2. Factor Analysis | Domino Data Science Dictionary (dominodatalab.com)

1

A latent variable is a variable that cannot be observed.