资本资产定价模型(CAPM) - 理论很丰满，现实很骨感

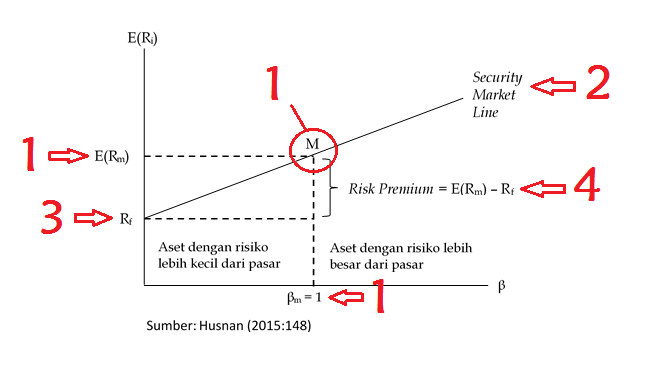
Fig. 2 资本资产定价模型(CAPM)

前言

自己懒得再造轮子，于是乎在国外某私人网站偷了幅图，看着觉得挺吊的，就拿来做封面了。说实话，资本资产定价模型(CAPM)是非常理论的东西，如果非科班出身，并非随便看看就能理解。虽说如此，还是看看其定义吧。

资本资产定价模型(CAPM)

资本资产定价模型

CAPM阐述了在投资者都采用马科维茨的理论进行投资管理的条件下市场均衡状态的形成，把资产的预期收益与预期风险之间的理论关系用一个简单的线性关系表达出来了，即认为一个资产的预期收益率与衡量该资产风险的一个尺度β值之间存在正相关关系。应该说，作为一种阐述风险资产均衡价格决定的理论，单一指数模型，或以之为基础的CAPM不仅大大简化了投资组合选择的运算过程，使马科维茨的投资组合选择理论朝现实世界的应用迈进了一大步，而且也使得证券理论从以往的定性分析转入定量分析，从规范性转入实证性，进而对证券投资的理论研究和实际操作，甚至整个金融理论与实践的发展都产生了巨大影响，成为现代金融学的理论基础。

预期回报率(Expected Return)公式

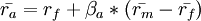
Fig. 3 单个股票或者股票组合的预期回报率(Expected Return)公式

• rf 是无风险回报率，纯粹的货币时间价值 – 无风险收益率（rf）的探讨和使用

• βa 是证券的Beta系数 – 巴菲特都不用beta值，你还用？!

• Rm 是市场期望回报率 (Expected Market Return)

• (Rm - rf) 是股票市场溢价 (Equity Market Premium) – 历史数据得出的股票风险溢价(ERP)的利弊

这个模型之所为伟大， 其实说白了，就是终于有一套理论模型能够确立资产的风险和资产收益率之间的关系。

理论很丰满

那么我们再看看其假设： 资本资产定价模型(CAPM)是建立在马科威茨模型基础上的，马科威茨模型的假设自然包含在其中：

1. 投资者希望财富越多愈好，效用是财富的函数，财富又是投资收益率的函数，因此可以认为效用为收益率的函数。

2. 投资者能事先知道投资收益率的概率分布为正态分布。

3. 投资风险用投资收益率的方差或标准差标识。

4. 影响投资决策的主要因素为期望收益率和风险两项。

5. 投资者都遵守主宰原则(Dominance rule)，即同一风险水平下，选择收益率较高的证券；同一收益率水平下，选择风险较低的证券。

资本资产定价模型(CAPM)的附加假设条件：

1. 可以在无风险折现率R的水平下无限制地借入或贷出资金。

2. 所有投资者对证券收益率概率分布的看法一致，因此市场上的效率边界只有一条。

3. 所有投资者具有相同的投资期限，而且只有一期。

4. 所有的证券投资可以无限制的细分，在任何一个投资组合里可以含有非整数股份。

5. 买卖证券时没有税负及交易成本。

6. 所有投资者可以及时免费获得充分的市场信息。

7. 不存在通货膨胀，且折现率不变。

8. 投资者具有相同预期，即他们对预期收益率、标准差和证券之间的协方差具有相同的预期值。

上述假设表明：第一，投资者是理性的，而且严格按照马科威茨模型的规则进行多样化的投资，并将从有效边界的某处选择投资组合；第二，资本市场是完美/完全市场，没有任何磨擦阻碍投资。

现实很骨感

总的来说，模型的假设是基于理性的投资者和完美市场的基础上。 这现实吗？！

假设投资者是理性的话，A股市场上就不会有什么追涨停、追退市股等疯狂行为。所以凯恩斯(John Maynard Keynes)才说出了这样的金句：

The market can remain irrational longer than you can remain solvent. 大概意思是：你破产了也等不到市场回归理性。

价值意义

虽说资本资产定价模型(CAPM)的假设条件过于理想和苛刻， 但它却解释了影响风险资产(股票)定价的三大主要因数：无风险收益率. 风险的价格和风险的计算单位。往后大多数的模型中凡是涉及投资者要求回报率(cost of equity)的，那么基本上都是通过资本资产定价模型(CAPM)得到，公式中的预期回报率(Ra)可以当作为投资者要求回报率(cost of equity)。

例如， 在文章股利贴现模型 - 戈登模型(Gordon Growth Model)的模型公式中的 r 就需要用到CAPM来计算。