Principal Component Analysis - 主成分分析
Contents
Principal Component Analysis - 主成分分析#
Factor Analysis
PCA is efficient in finding the components that maximize variance. This is great if we are interested in reducing the number of variables while keeping a maximum of variance.
– Joos Korstanje
一、目的#
PCA(Principal Component Analysis)目的在于减少数据集中的指标(变量)数量的同时尽可能地保留指标信息。
一般来说,一个数据集中往往包含了大量指标(变量),在正常的情况下是很难逐个指标(变量)去分析、观察、理解,PCA通常将大量的指标(变量)划分至不同的成分,从而达到降维的效果(减少变量),同时也保留了数据的主要特征(方差最大化)。
二、原理#
PCA 在统计学上的定义在于,在线性组合中寻找含有最大方差的原始变量。
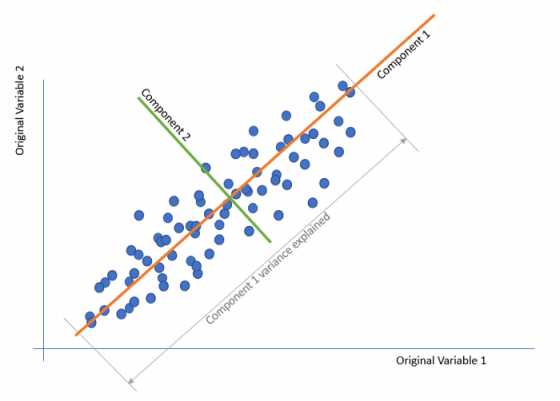
Fig. 22 Schematic model of PCA By Joos Korstanje.#
这个过程中,我们将创建一个名为,z,的新组合(Component)。 这个 组合z 将基于我们的原始指标(变量)(X1,X2,…)乘以我们每个变量(u1,u2,…)的权重来计算。
这可以写成 z = Xu。
这里的目标是找到可以将 z 的方差最大化的 u 值。这个问题在数学上被称为拉格朗日乘数的约束优化(constrained optimization using Lagrange Multiplier)。
三、何时使用PCA or FA#
1、Principal Component Analysis - 主成分分析#
数据集中的指标(变量)数量过多,不便于数据分析
假设数据集中没有任何测量误差或噪声noise
2、Factor Analysis - 因子分析#
对数据集的变量降维(减少变量)没有兴趣
希望找出数据集中某些最具解释力度的变量
例如,在心理学中:将很长的个性测试反馈减少为只有少量的个性特质
例如,在市场营销中:将包含了各种各样问题的产品评估问卷调查归类为几个因子,用于产品改进
四、Python实现方式#
from sklearn.decomposition import PCA
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
my_pca = PCA(n_components=2)
my_pca.fit(X)
print(my_pca.explained_variance_ratio_)
print(my_pca.singular_values_)
参考:
