Factor Analysis
Contents
Factor Analysis#
文章说明:
这文章为Avinash Navlani在datacamp写的关于FA的入门介绍
import numpy as np
import pandas as pd
from factor_analyzer import FactorAnalyzer
import matplotlib.pyplot as plt
导入数据#
这是关于人格的数据集
数据集介绍: https://vincentarelbundock.github.io/Rdatasets/doc/psych/bfi.html
数据集下载: https://vincentarelbundock.github.io/Rdatasets/datasets.html
df = pd.read_csv("https://vincentarelbundock.github.io/Rdatasets/csv/psych/bfi.csv")
# df= pd.read_csv("bfi.csv")
数据说明:
这是从国际人格项目库(ipip.ori.org)中提取的25个人格项目报告
其中包含来自 2800 个受试者的数据,用于规模构建、因子分析和项目响应理论分析的演示集
其中还包括三个额外的人口统计变量(性别,教育和年龄)
数据所包含的 28 个问题:
A1 我对别人的感受漠不关心。(q_146)
A2 询问他人的幸福感。(q_1162)
A3 知道如何安慰别人。(q_1206)
A4 爱孩子。(q_1364)
A5 让人们感到安心。(q_1419)
C1 我的工作非常严格。(q_124)
…
Tip
剔除人口统计变量(性别,教育和年龄)这个3个变量特征,前25个变量特征实际上是由五个隐性变量(latent variables)组成:亲和力,尽责性,外向性,神经质和开放性。
c(“-A1”,“A2”,“A3”,“A4”,“A5”) => 亲和力
c(“C1”,“C2”,“C3”,“-C4”,“-C5”) => 尽责性
c(“-E1”,“-E2”,“E3”,“E4”,“E5”) => 外向性
c(“N1”,“N2”,“N3”,“N4”,“N5”) => 神经质
c(“O1”,“-O2”,“O3”,“O4”,“-O5”) => 开放性
# 剔除不必要的人口统计变量特征(性别,教育和年龄)
df.drop(['Unnamed: 0', 'gender', 'education', 'age'],axis=1,inplace=True)
# 去除缺失数据
df.dropna(inplace=True)
df.head()
| A1 | A2 | A3 | A4 | A5 | C1 | C2 | C3 | C4 | C5 | ... | N1 | N2 | N3 | N4 | N5 | O1 | O2 | O3 | O4 | O5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2.0 | 4.0 | 3.0 | 4.0 | 4.0 | 2.0 | 3.0 | 3.0 | 4.0 | 4.0 | ... | 3.0 | 4.0 | 2.0 | 2.0 | 3.0 | 3.0 | 6 | 3.0 | 4.0 | 3.0 |
| 1 | 2.0 | 4.0 | 5.0 | 2.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | 4.0 | ... | 3.0 | 3.0 | 3.0 | 5.0 | 5.0 | 4.0 | 2 | 4.0 | 3.0 | 3.0 |
| 2 | 5.0 | 4.0 | 5.0 | 4.0 | 4.0 | 4.0 | 5.0 | 4.0 | 2.0 | 5.0 | ... | 4.0 | 5.0 | 4.0 | 2.0 | 3.0 | 4.0 | 2 | 5.0 | 5.0 | 2.0 |
| 3 | 4.0 | 4.0 | 6.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | 5.0 | 5.0 | ... | 2.0 | 5.0 | 2.0 | 4.0 | 1.0 | 3.0 | 3 | 4.0 | 3.0 | 5.0 |
| 4 | 2.0 | 3.0 | 3.0 | 4.0 | 5.0 | 4.0 | 4.0 | 5.0 | 3.0 | 2.0 | ... | 2.0 | 3.0 | 4.0 | 4.0 | 3.0 | 3.0 | 3 | 4.0 | 3.0 | 3.0 |
5 rows × 25 columns
df.shape
(2436, 25)
充分性测试(Adequacy Test)#
在做因子分析之前, 我们需要先做充分性检测, 判断数据集中是否存在因子(factor):
Bartlett's Test: 是用来检测已知(可观察)变量的相关矩阵是否单位矩阵,如果不是,那么变量之间存在相关性, 可采用因子分析Kaiser-Meyer-Olkin(KMO) Test: 检测数据对因子分析的适用性。KMO 值的范围介于 0 和 1 之间。 KMO数值越大,变量间的相关性越强。KMO 值需要大于 0.6 才视为适用
# Bartlett's Test
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
chi_square_value,p_value=calculate_bartlett_sphericity(df)
chi_square_value, p_value
(18146.06557723503, 0.0)
说明:p_value=0, 表明数据变量间的相关矩阵不是单位矩阵,具有显著的关联性,可采用因子分析. p_value需要少于0.5
# Kaiser-Meyer-Olkin(KMO) Test
from factor_analyzer.factor_analyzer import calculate_kmo
kmo_all,kmo_model=calculate_kmo(df)
print(kmo_model)
0.8486452309468397
说明: KMO 值大于 0.6 ,符合因子分析的适用性
选择因子个数#
# 数据集中共有25个变量,我们需要考虑究竟需要归集为多少个因子是最合适的
fa = FactorAnalyzer(25, rotation=None)
fa.fit(df)
# 计算相关矩阵的特征值
ev, v = fa.get_eigenvalues()
ev
array([5.13431118, 2.75188667, 2.14270195, 1.85232761, 1.54816285,
1.07358247, 0.83953893, 0.79920618, 0.71898919, 0.68808879,
0.67637336, 0.65179984, 0.62325295, 0.59656284, 0.56309083,
0.54330533, 0.51451752, 0.49450315, 0.48263952, 0.448921 ,
0.42336611, 0.40067145, 0.38780448, 0.38185679, 0.26253902])
# 可视化
plt.scatter(range(1,df.shape[1]+1),ev)
plt.plot(range(1,df.shape[1]+1),ev)
plt.title('Scree Plot')
plt.xlabel('Factors')
plt.ylabel('Eigenvalue')
plt.grid()
plt.show()
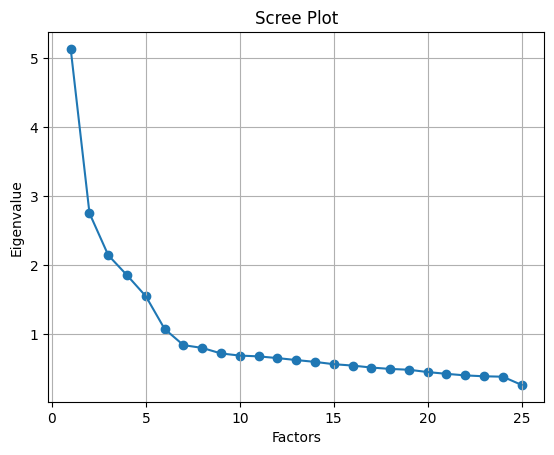
如图,这里显示有 6 个因子的特征值是大于 1。这意味着我们只需要选择6个因子(或未观察到的变量)。
因子分析(Factor Analysis)#
#指定矩阵旋转方式为varimax,实现方差最大化
fa = FactorAnalyzer(6, rotation="varimax")
fa.fit(df)
FactorAnalyzer(n_factors=6, rotation='varimax', rotation_kwargs={})In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
FactorAnalyzer(n_factors=6, rotation='varimax', rotation_kwargs={})# 25*6(变量个数*因子个数),查看成分矩阵loadings_
fa.loadings_
array([[ 9.52197423e-02, 4.07831572e-02, 4.87338847e-02,
-5.30987346e-01, -1.13057329e-01, 1.61216351e-01],
[ 3.31312762e-02, 2.35538039e-01, 1.33714394e-01,
6.61140977e-01, 6.37337873e-02, -6.24353724e-03],
[-9.62088396e-03, 3.43008173e-01, 1.21353367e-01,
6.05932695e-01, 3.39902656e-02, 1.60106427e-01],
[-8.15175586e-02, 2.19716720e-01, 2.35139531e-01,
4.04594039e-01, -1.25338019e-01, 8.63557023e-02],
[-1.49615885e-01, 4.14457674e-01, 1.06382165e-01,
4.69698291e-01, 3.09765728e-02, 2.36519342e-01],
[-4.35840225e-03, 7.72477524e-02, 5.54582255e-01,
7.51069593e-03, 1.90123730e-01, 9.50350463e-02],
[ 6.83300837e-02, 3.83703838e-02, 6.74545451e-01,
5.70549874e-02, 8.75925915e-02, 1.52775080e-01],
[-3.99936733e-02, 3.18673004e-02, 5.51164439e-01,
1.01282241e-01, -1.13380873e-02, 8.99628315e-03],
[ 2.16283366e-01, -6.62407738e-02, -6.38475489e-01,
-1.02616940e-01, -1.43846475e-01, 3.18358899e-01],
[ 2.84187245e-01, -1.80811697e-01, -5.44837676e-01,
-5.99548223e-02, 2.58370942e-02, 1.32423445e-01],
[ 2.22797940e-02, -5.90450890e-01, 5.39149061e-02,
-1.30850531e-01, -7.12045794e-02, 1.56582656e-01],
[ 2.33623566e-01, -6.84577632e-01, -8.84970712e-02,
-1.16715665e-01, -4.55610413e-02, 1.15065401e-01],
[-8.95006159e-04, 5.56774179e-01, 1.03390347e-01,
1.79396481e-01, 2.41179904e-01, 2.67291315e-01],
[-1.36788076e-01, 6.58394906e-01, 1.13798005e-01,
2.41142961e-01, -1.07808203e-01, 1.58512851e-01],
[ 3.44895882e-02, 5.07535081e-01, 3.09812528e-01,
7.88042870e-02, 2.00821351e-01, 8.74730257e-03],
[ 8.05805940e-01, 6.80113035e-02, -5.12637874e-02,
-1.74849359e-01, -7.49771190e-02, -9.62661720e-02],
[ 7.89831685e-01, 2.29582935e-02, -3.74768701e-02,
-1.41134482e-01, 6.72646116e-03, -1.39822612e-01],
[ 7.25081218e-01, -6.56869338e-02, -5.90394375e-02,
-1.91838176e-02, -1.06635546e-02, 6.24953366e-02],
[ 5.78318850e-01, -3.45072325e-01, -1.62173861e-01,
4.03124702e-04, 6.29164834e-02, 1.47551243e-01],
[ 5.23097072e-01, -1.61675117e-01, -2.53049777e-02,
9.01247903e-02, -1.61891978e-01, 1.20049478e-01],
[-2.00040179e-02, 2.25338562e-01, 1.33200799e-01,
5.17793807e-03, 4.79477217e-01, 2.18689834e-01],
[ 1.56230108e-01, -1.98151980e-03, -8.60468495e-02,
4.39891065e-02, -4.96639673e-01, 1.34692973e-01],
[ 1.18510152e-02, 3.25954482e-01, 9.38796109e-02,
7.66416468e-02, 5.66128048e-01, 2.10777220e-01],
[ 2.07280571e-01, -1.77745714e-01, -5.67146619e-03,
1.33655572e-01, 3.49227137e-01, 1.78068366e-01],
[ 6.32343665e-02, -1.42210625e-02, -4.70592287e-02,
-5.75607778e-02, -5.76742634e-01, 1.35935872e-01]])
# 可视化
import seaborn as sns
df_cm = pd.DataFrame(fa.loadings_, index=df.columns)
plt.figure(figsize = (14,14))
ax = sns.heatmap(df_cm, annot=True, cmap="BuPu")
ax.xaxis.set_tick_params(labelsize=15)
ax.yaxis.set_tick_params(labelsize=15)
plt.title('Factor Analysis', fontsize='xx-large')
Text(0.5, 1.0, 'Factor Analysis')
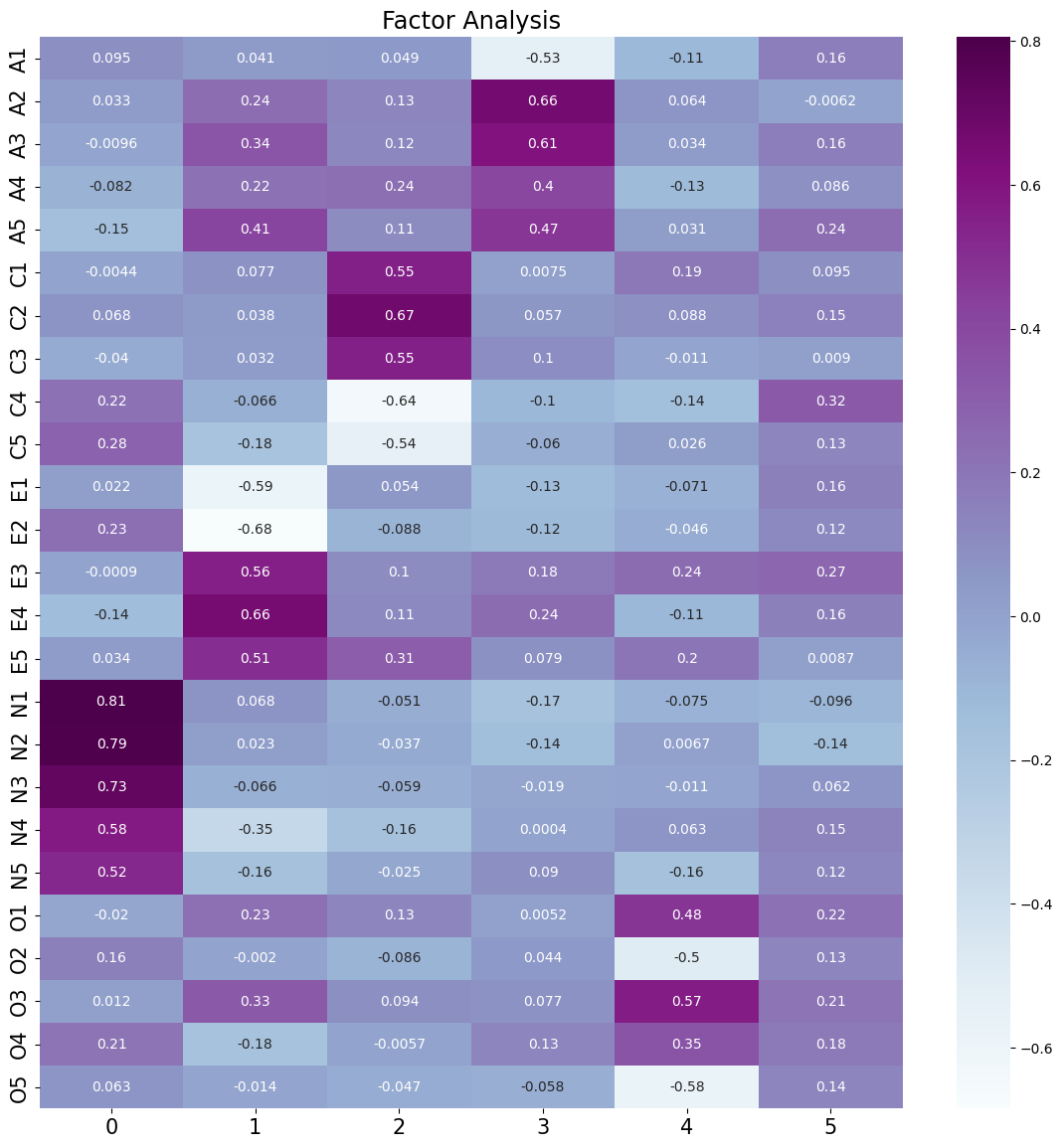
说明:
每一个变量都可以由6个隐变量所表示
A1 = 0.0095F1 + 0.041F2 + 0.049F3 + -0.53F4 + -0.11F5 + 0.16F6
A2 = 0.033F1 + 0.24F2 + 0.13F3 + 0.66F4 + 0.064F5 + -0.0062F6
# 累计贡献率
pd.DataFrame(fa.get_factor_variance(),index=['variance','proportional_variance','cumulative_variances'], columns=[f"factor{x}" for x in range(1,7)])
| factor1 | factor2 | factor3 | factor4 | factor5 | factor6 | |
|---|---|---|---|---|---|---|
| variance | 2.726989 | 2.602239 | 2.073471 | 1.713499 | 1.504831 | 0.630297 |
| proportional_variance | 0.109080 | 0.104090 | 0.082939 | 0.068540 | 0.060193 | 0.025212 |
| cumulative_variances | 0.109080 | 0.213169 | 0.296108 | 0.364648 | 0.424841 | 0.450053 |
总方差贡献:variance – The factor variances
方差贡献率:proportional_variance – The proportional factor variances
累积方差贡献率:cumulative_variances – The cumulative factor variances
说明: 6 个因子可以解释累积 45% 方差
转成新变量(Transform)#
说明:通过因子分析,得到了6个新的特征可以描述原始数据集;因此,我们可以将原始数据转成6个新的特征:
pd.DataFrame(fa.transform(df))
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | -0.350506 | 0.033583 | -1.300285 | -0.512135 | -1.429475 | -0.693275 |
| 1 | 0.081829 | 0.570999 | -0.612138 | -0.201342 | -0.243352 | -0.016911 |
| 2 | 0.564684 | 0.327277 | 0.083021 | -0.824345 | 0.210169 | -0.236172 |
| 3 | -0.232325 | 0.071300 | -0.963956 | -0.268270 | -1.187286 | 0.834096 |
| 4 | -0.337498 | 0.364706 | -0.137084 | -0.798106 | -0.675213 | -0.190357 |
| ... | ... | ... | ... | ... | ... | ... |
| 2431 | 1.408181 | -1.159475 | -0.151991 | -0.935139 | 0.526645 | -0.550600 |
| 2432 | 0.710526 | 0.302318 | -0.467326 | -0.568166 | 0.924407 | 0.677355 |
| 2433 | -0.166061 | 0.702602 | 0.762533 | -1.000853 | 0.941894 | -0.427568 |
| 2434 | 0.942174 | 0.700984 | 0.119800 | -2.207187 | 0.682026 | -0.193905 |
| 2435 | -1.531255 | -1.424258 | -0.260095 | -1.465039 | 0.068920 | -1.428128 |
2436 rows × 6 columns

