VaR模型 - 用方差-协方差计算VaR
Contents
VaR模型 - 用方差-协方差计算VaR#
用方差-协方差计算VaR
用方差-协方差计算VaR的思路跟历史模拟法来计算VaR是不一样的,前者是根据股票某时间段的均值(mean),标准差(standard deviation),根据这两个值再重新算出正态分布图,然后然后根据置信区间来确定在险价值;而后者是先计算出某只股票某段时间的整体回报率和波动, 然后根据置信区间的百分比,如10%、5%或 1% 来确定在险价值。
正如我刚刚所提到,用方差-协方差来计算VaR是基于正态分布作为前提,所以这也是缺点之一。
import tushare as ts
import pandas as pd
import numpy as np
import scipy.stats
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
pro = ts.pro_api('xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx') #这里需要填写你注册好的Tushare的TOKEN凭证
/tmp/ipykernel_2317/3543896033.py:6: MatplotlibDeprecationWarning: The seaborn styles shipped by Matplotlib are deprecated since 3.6, as they no longer correspond to the styles shipped by seaborn. However, they will remain available as 'seaborn-v0_8-<style>'. Alternatively, directly use the seaborn API instead.
plt.style.use('seaborn-white')
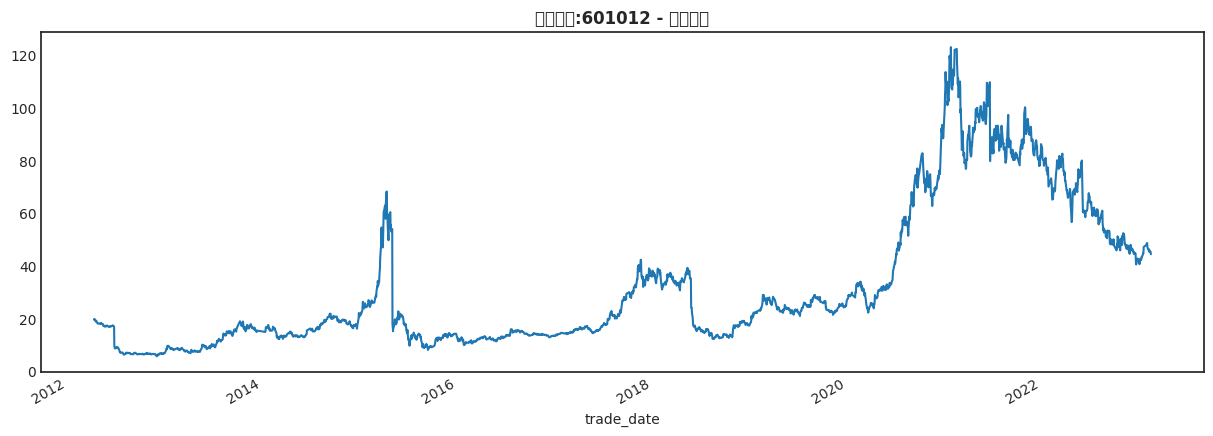
通过调用tushare获取股票601012(隆基股份)的股票数据,这里不设置日期,那么默认获取Tushare提供的历史数据。
ticker_data = pro.daily(ts_code='601012.SH')
print('数据量:',len(ticker_data))
ticker_data.head(5)
数据量: 2598
| ts_code | trade_date | open | high | low | close | pre_close | change | pct_chg | vol | amount | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 601012.SH | 20230216 | 45.10 | 45.60 | 44.15 | 44.44 | 45.24 | -0.80 | -1.7683 | 689097.70 | 3099747.920 |
| 1 | 601012.SH | 20230215 | 45.62 | 46.30 | 45.08 | 45.24 | 45.44 | -0.20 | -0.4401 | 566250.95 | 2581315.291 |
| 2 | 601012.SH | 20230214 | 45.80 | 45.85 | 44.92 | 45.44 | 45.62 | -0.18 | -0.3946 | 578539.49 | 2615525.826 |
| 3 | 601012.SH | 20230213 | 45.40 | 45.80 | 45.10 | 45.62 | 45.38 | 0.24 | 0.5289 | 476689.45 | 2170518.460 |
| 4 | 601012.SH | 20230210 | 46.24 | 46.24 | 45.15 | 45.38 | 46.24 | -0.86 | -1.8599 | 587482.78 | 2673747.825 |
从上面可以看出,序号并不是以时间作为单位的。那么我们首先需要将trade_date转为datetime格式,然后设置为序号以便于画图。
ticker_data['trade_date'] = pd.to_datetime(ticker_data['trade_date'],format='%Y%m%d')
ticker_data.set_index('trade_date', inplace=True)
returns = ticker_data["close"].pct_change().dropna()
plt.figure(figsize=(15, 5))
plt.title("股票代码:601012 - 隆基股份", weight='bold')
ticker_data['close'].plot()
<Axes: title={'center': '股票代码:601012 - 隆基股份'}, xlabel='trade_date'>
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 32929 (\N{CJK UNIFIED IDEOGRAPH-80A1}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 31080 (\N{CJK UNIFIED IDEOGRAPH-7968}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 20195 (\N{CJK UNIFIED IDEOGRAPH-4EE3}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 30721 (\N{CJK UNIFIED IDEOGRAPH-7801}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 38534 (\N{CJK UNIFIED IDEOGRAPH-9686}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 22522 (\N{CJK UNIFIED IDEOGRAPH-57FA}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 20221 (\N{CJK UNIFIED IDEOGRAPH-4EFD}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 32929 (\N{CJK UNIFIED IDEOGRAPH-80A1}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 31080 (\N{CJK UNIFIED IDEOGRAPH-7968}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 20195 (\N{CJK UNIFIED IDEOGRAPH-4EE3}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 30721 (\N{CJK UNIFIED IDEOGRAPH-7801}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 38534 (\N{CJK UNIFIED IDEOGRAPH-9686}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 22522 (\N{CJK UNIFIED IDEOGRAPH-57FA}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 20221 (\N{CJK UNIFIED IDEOGRAPH-4EFD}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
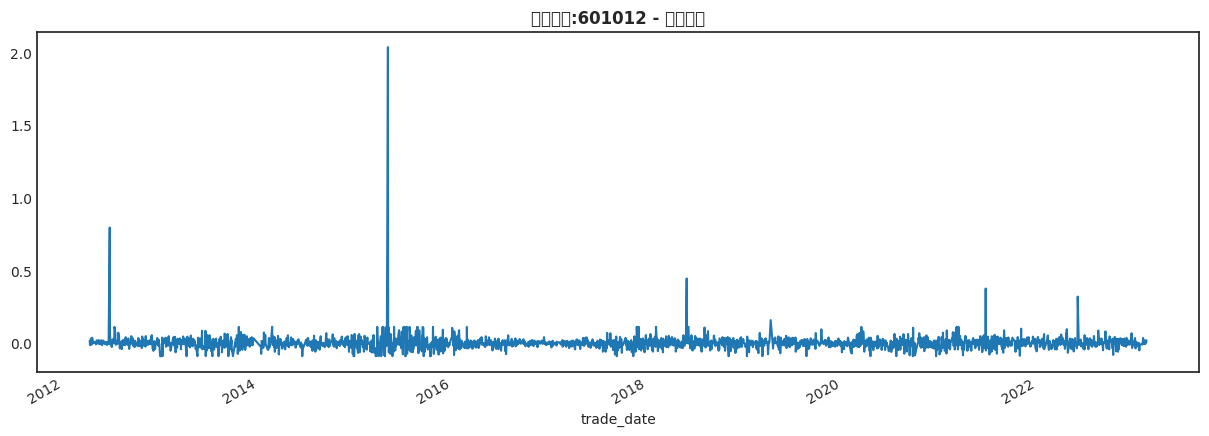
下面将画出每日收盘价的百分比变化图:
plt.figure(figsize=(15, 5))
ticker_data["close"].pct_change().plot()
plt.title("股票代码:601012 - 隆基股份", weight='bold');
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 32929 (\N{CJK UNIFIED IDEOGRAPH-80A1}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 31080 (\N{CJK UNIFIED IDEOGRAPH-7968}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 20195 (\N{CJK UNIFIED IDEOGRAPH-4EE3}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 30721 (\N{CJK UNIFIED IDEOGRAPH-7801}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 38534 (\N{CJK UNIFIED IDEOGRAPH-9686}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 22522 (\N{CJK UNIFIED IDEOGRAPH-57FA}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 20221 (\N{CJK UNIFIED IDEOGRAPH-4EFD}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 32929 (\N{CJK UNIFIED IDEOGRAPH-80A1}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 31080 (\N{CJK UNIFIED IDEOGRAPH-7968}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 20195 (\N{CJK UNIFIED IDEOGRAPH-4EE3}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 30721 (\N{CJK UNIFIED IDEOGRAPH-7801}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 38534 (\N{CJK UNIFIED IDEOGRAPH-9686}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 22522 (\N{CJK UNIFIED IDEOGRAPH-57FA}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 20221 (\N{CJK UNIFIED IDEOGRAPH-4EFD}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
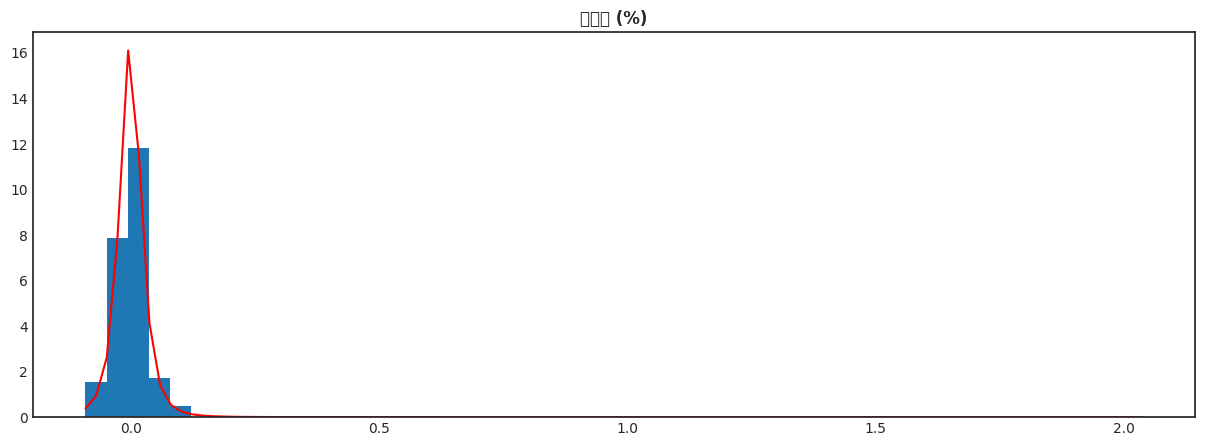
方差-协方差计算VaR#
mean = returns.mean()
sigma = returns.std()
tdf, tmean, tsigma = scipy.stats.t.fit(returns)
support = np.linspace(returns.min(), returns.max(), 100)
plt.figure(figsize=(15, 5))
plt.hist(returns,bins=50, density=True)
plt.plot(support, scipy.stats.t.pdf(support, loc=tmean, scale=tsigma, df=tdf), "r-") #pdf(x, df, loc=0, scale=1) Probability density function.
plt.title("回报率 (%)", weight='bold');
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 22238 (\N{CJK UNIFIED IDEOGRAPH-56DE}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 25253 (\N{CJK UNIFIED IDEOGRAPH-62A5}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/events.py:89: UserWarning: Glyph 29575 (\N{CJK UNIFIED IDEOGRAPH-7387}) missing from current font.
func(*args, **kwargs)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 22238 (\N{CJK UNIFIED IDEOGRAPH-56DE}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 25253 (\N{CJK UNIFIED IDEOGRAPH-62A5}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
/opt/hostedtoolcache/Python/3.8.16/x64/lib/python3.8/site-packages/IPython/core/pylabtools.py:152: UserWarning: Glyph 29575 (\N{CJK UNIFIED IDEOGRAPH-7387}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)
#ppf(q, df, loc=0, scale=1) Percent point function (inverse of cdf — percentiles).
scipy.stats.norm.ppf(0.05, mean, sigma)
-0.09022617922983799
解释
用股票601012的方差-协方差得出每日收益率为-9.34%, 这意味着95%的机率这只股票单日的损失不高于9.34%. 如果你投资100万来计算绝对金额,一日5% VaR为0.0934 * 100万 = 9.34万。

