投资组合的夏普比率(portfolio’s Sharpe Ratio) 的理论和实践#

前言#

如果平时有使用米筐、优矿等量化平台，你会发现每个量化策略的运行结果必定出现夏普比率这个值。其实这个值是什么来的、又有什么作用呢？

理论#

在投资行业我们听到最多的一句莫过于“风险越大，收益越大”。这一句简单的话正好就解释了为啥存银行的收益率远远低于买股票的收益率，就是因为风险和收益是成正比的关系。夏普比率（Sharpe Ratio）的出现正好可以解决这个风险和收益之间的关系，同样的风险下收益最大化。这个该如何理解呢？打个比方，假如我把钱都买了股票，假设股票市场里所有股票的风险都是一样的，为啥我不投资一个收益最大化的股票呢？！

formula — Fig. 17 夏普比率(portfolio’s Sharpe Ratio)的基本公式, 从知乎借来的图#

这是收益和风险的正比关系，我们不可能买着银行的理财产品但承受着股票市场的风险。但这个所谓“正比关系”该如何去衡量呢？这时候我们就可以利用夏普比率(Sharpe Ratio) 来评估。

从表达式可以看出，公式主要分为上下两个部分。上面的分子部分主要是投资收益，下面的分母部分主要是投资风险，即一定时间段内投资产品的波动率。

先来看看分子部分的投资收益，为啥我们的投资回报还要扣除无风险收益率（Rf）呢？因为在投资行业中，我们假设我们的投资收益是高于购买长期国债（假设国家不会倒闭，所以无风险）的收益，正因为我们的“正确”的投资决策才产生的收益，这部分收益才是我们真正的收益。
下面的分母部分就是投资产品在投资期内的波动率，这里所谓的波动率实际上就是我们统计学上的标准差。至于啥是标准差。。。

注意事项#

在计算夏普比率(Sharpe Ratio)的时候，我们需要注意：

收益和风险的计算周期需要一致。例如，你计算的收益回报是月度的，那么波动率的时间单位也需要是月度的，然后再转化为年度。
夏普比率(Sharpe Ratio)不适用于单只股票；一般是基于投资组合来计算的。
转换标准差的时间单位是，记得带上根号。例如，月度标准差是10，那么年度标准差就是10*√12。

实践#

步骤#

首先调用Tushare的API 获取股票数据；
计算投资组合的整体回报率；
计算投资组合的整体波动率。

过程#

在2个月前我写过一篇关于用股息分红来选股的文章：，最后得出了28只股票：

['000507.SZ', '000568.SZ', '000661.SZ', '000733.SZ', '000738.SZ', '000860.SZ', '002026.SZ', '002088.SZ', '002189.SZ', '002360.SZ', '002685.SZ', '300121.SZ', '300269.SZ', '300308.SZ', '600277.SH', '600323.SH', '600326.SH', '600377.SH', '600566.SH', '600567.SH', '600592.SH', '600660.SH', '600737.SH', '600757.SH', '600995.SH', '601100.SH', '601588.SH', '603869.SH']

既然这样，我就直接用这28只股票里面的前8只股票来当示范例子。当然，你也可以随便挑几只其他的股票来计算。

import tushare as ts
import pandas as pd
import math
import matplotlib.pyplot as plt

pro = ts.pro_api('xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx') #这里需要填写你注册好的Tushare的TOKEN凭证

下面挑了8只股票，然后allocations是指每只股票的投入比例，这里我是按照平均分配，意味着如果我有￥80，每只股票的投入金额为￥10

stock_tickers = ['000507.SZ', '000568.SZ', '000661.SZ', '000733.SZ', '000738.SZ', '000860.SZ', '002026.SZ', '002088.SZ']
allocations = [1/len(stock_tickers)]*len(stock_tickers) #投资比例为平均分配
investment = 10000   #投资总金额为1万元

#先建立一个字典，用来存储股票对应的股票数据
all_data = {} 

数据获取和数据清洗#

for ticker,allocation in zip(stock_tickers,allocations):
    #获取代码的数据，周期为1年
    ticker_df = pro.daily(ts_code=ticker, start_date='20200101', end_date='20220209').sort_values('trade_date',ascending=True)
    #设置trade_date为datetime形式
    ticker_df['trade_date'] = pd.to_datetime(ticker_df['trade_date'])
    #设置trade_date为index
    ticker_df.set_index('trade_date',inplace=True)
    #我们假设2018年1月2号开始投资，并一直持有，往后每日的股价变化除以初始的股票价格就得出每只股票的金额变化
    ticker_df['norm return'] = ticker_df['close'] / ticker_df.iloc[0]['close']
    #然后再根据上面得出的百分比乘以我们每只股票的资产配置比例（这里是假设是平均分配）
    ticker_df['allocation'] = ticker_df['norm return'] * allocation
    #然后再乘以投资金额，就可以得出每只股票的资产配置的绝对金额
    ticker_df['position'] = ticker_df['allocation']*investment
    
    all_data[ticker] = ticker_df
#用for循环遍历股票价格并转换为dataframe的形式
portfolio_val= pd.DataFrame({tic: data['position']
                    for tic, data in all_data.items()})
#将所有仓位都加起来得出总仓位
portfolio_val['TotalPosition'] = portfolio_val.sum(axis=1)
portfolio_val.head()

	000507.SZ	000568.SZ	000661.SZ	000733.SZ	000738.SZ	000860.SZ	002026.SZ	002088.SZ	TotalPosition
trade_date
2020-01-02	1250.000000	1250.000000	1250.000000	1250.000000	1250.000000	1250.000000	1250.000000	1250.000000	10000.000000
2020-01-03	1247.990354	1254.973669	1333.634720	1289.106940	1267.816954	1226.891970	1257.102273	1252.314815	10129.831694
2020-01-06	1239.951768	1252.486834	1343.891275	1316.837315	1268.754689	1219.911419	1266.571970	1248.842593	10157.247863
2020-01-07	1243.971061	1258.045641	1383.872061	1326.080774	1273.443361	1249.277874	1268.939394	1267.361111	10270.991277
2020-01-08	1219.855305	1241.222937	1379.831600	1316.837315	1299.699925	1239.408820	1250.000000	1233.796296	10180.652199

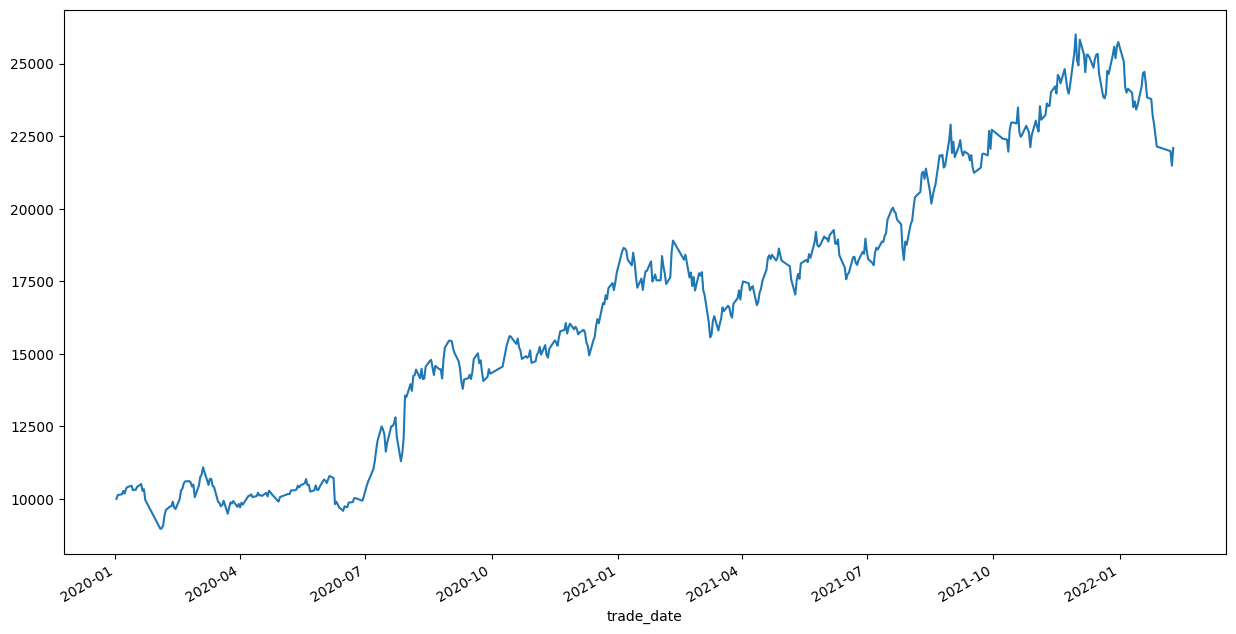
下面画出总仓位的资金变化图，起始金额为1万元。

portfolio_val['TotalPosition'].plot(figsize=(15,8))

<Axes: xlabel='trade_date'>

../_images/portfolio-sharpe-ratio_9_1.png

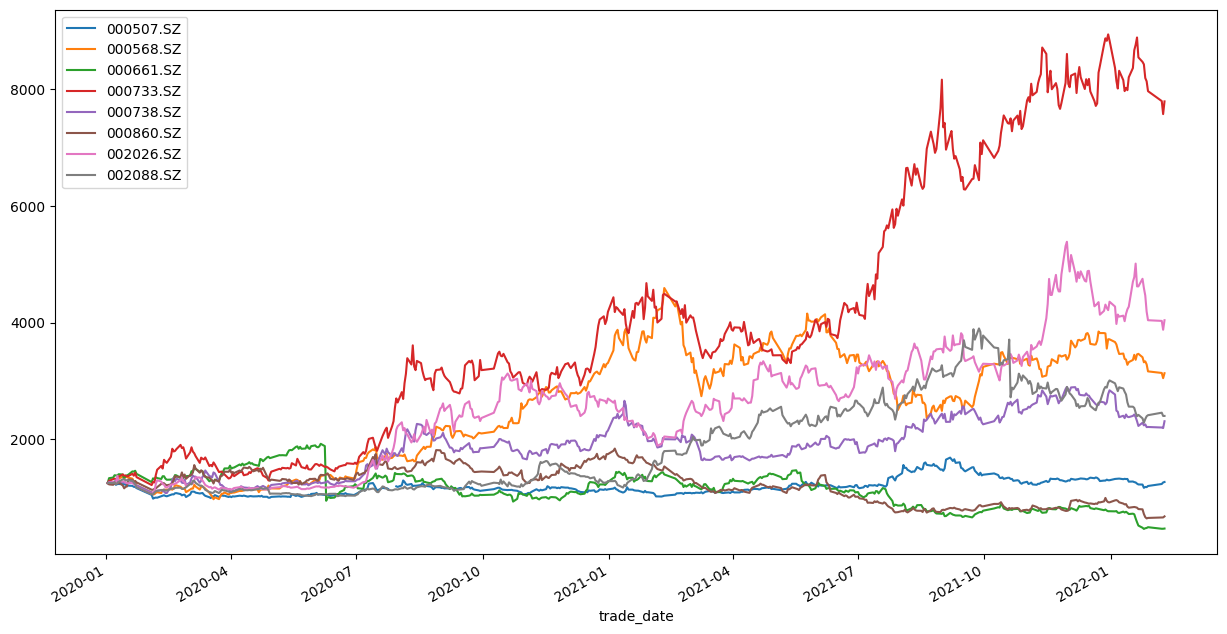
画出每只股票的资金#

portfolio_val.drop('TotalPosition',axis=1).plot(figsize=(15,8))

<Axes: xlabel='trade_date'>

../_images/portfolio-sharpe-ratio_11_1.png

cumulative_return = 100 * ( portfolio_val['TotalPosition'].iloc[-1] / portfolio_val['TotalPosition'].iloc[0] -1)
print('累计总回报： {:.2f}% '.format(cumulative_return))

累计总回报： 120.93%

portfolio_val.tail(1)

	000507.SZ	000568.SZ	000661.SZ	000733.SZ	000738.SZ	000860.SZ	002026.SZ	002088.SZ	TotalPosition
trade_date
2022-02-09	1268.086817	3133.118783	470.021474	7792.235495	2309.63991	678.557674	4041.193182	2400.462963	22093.316297

portfolio_val['Daily Return'] = portfolio_val['TotalPosition'].pct_change()
portfolio_val.head()

	000507.SZ	000568.SZ	000661.SZ	000733.SZ	000738.SZ	000860.SZ	002026.SZ	002088.SZ	TotalPosition	Daily Return
trade_date
2020-01-02	1250.000000	1250.000000	1250.000000	1250.000000	1250.000000	1250.000000	1250.000000	1250.000000	10000.000000	NaN
2020-01-03	1247.990354	1254.973669	1333.634720	1289.106940	1267.816954	1226.891970	1257.102273	1252.314815	10129.831694	0.012983
2020-01-06	1239.951768	1252.486834	1343.891275	1316.837315	1268.754689	1219.911419	1266.571970	1248.842593	10157.247863	0.002706
2020-01-07	1243.971061	1258.045641	1383.872061	1326.080774	1273.443361	1249.277874	1268.939394	1267.361111	10270.991277	0.011198
2020-01-08	1219.855305	1241.222937	1379.831600	1316.837315	1299.699925	1239.408820	1250.000000	1233.796296	10180.652199	-0.008796

计算夏普比率#

### 下面将计算夏普比率，利用每日平均回报率除以其标准差
Sharpe_Ratio = portfolio_val['Daily Return'].mean() / portfolio_val['Daily Return'].std()
Sharpe_Ratio

0.08594024115798166

年化夏普比率#

### 上面得出的夏普比率是以日为单位，我们需要将其年化
# 其实就是分子的回报率乘以252日，然后除以√252
Annual_Sharpe_Ratio = Sharpe_Ratio *252/math.sqrt(252)
Annual_Sharpe_Ratio

1.3642590343016223

我们最后得出的年化夏普比率为 1.3642590343016223

by 柯西君_BingWong， cnVaR.cn

cn{VaR} - Value at Risk

投资组合的夏普比率(portfolio’s Sharpe Ratio) 的理论和实践

Contents