预测SP500指数走势
Contents
预测SP500指数走势#
一、前言#
作者:Griddb
标题:Modelling S&P 500 Index Price Based on U.S. Economic Indicators using Python and GridDB
目的:利用机器学习中的Regression Model 基于美国经济指标预测SP500走势
源码地址:无
数据源:
finance.yahoo.comandfred.stlouisfed.org
声明
本文只是出于学习的目的将其翻译成中文并附上一定的注释,并没有打算将其用作盈利的目的。
原文并没有提供原始数据集,我通过作者提供的数据出处,收集数据并清洗后放在文件夹中
由于yahoo finance上获取的SP500 index数据只有1985年打后的,所以跟原文的数据有一点出入
这里没有使用GridDB数据库,而是直接通过csv格式读取数据
数据集的获取方式放到文章的最后
二、研究目的#
经济指标已被用于许多的研究当中,而且很多的统计方法都结合了这些数据用于预测股票价格。本文的目的是根据美国经济指标对标准普尔500指数的月度价格进行建模, 然后执行统计测试,最后构建机器学习模型。
三、数据指标处理#
对于SP500指数来说,对其影响最大的指标可归纳为以下类别:一般宏观经济指标,劳动力市场指标(失业率和就业报告),房地产指标,信贷市场指标,货币供应指标,消费者(家庭)金融行为指标和商品市场指标。
数据周期为 1985-01-01 至 2022-06-01 之间
SP500指数收盘价和美国经济指标数据频率均为月度
数据集各变量(指标)的描述:
标准普尔500指数各月价格(单位:美元)
SP500利率,美国贴现率(单位:每年百分比)
INTDSRUSM193N商业和工业贷款,所有商业银行(单位:数十亿美元)
BUSLOANS银行优惠贷款利率(单位:百分比)
MPRIME联邦基金有效利率(联邦基金利率是存款机构隔夜交易联邦资金的利率。(单位:百分比)
FEDFUNDS流通中的货币(单位:数十亿美元)
CURRCIR个人储蓄率(个人储蓄占个人可支配收入(DPI)的百分比,通常称为“个人储蓄率”,计算为个人储蓄与DPI的比率。(单位:百分比)
PSAVERT在许可证发放地点授权的新私人住房单位:总单位(单位:数十亿美元)
PERMIT工业生产:总指数(工业生产指数(INDPRO)是衡量位于美国制造业,采矿业,电力和天然气公用事业的所有设施的实际产出的经济指标)(单位:指数2017 = 100)
INDPRO个人储蓄(单位:数十亿美元)
PMSAVE机动车零售:国内汽车 (单位:百万辆)
DAUTOSAAR失业水平 (单位: 数千人)
UNEMPLOY所有城市居民消费价格指数:美国城市平均值的所有项目(单位:指数1982-1984=100)
CPIAUCSL
上述数据集除了SP500之外,都可以单独从fred.stlouisfed.org上免费下载得到;而SP500可以从需要从finance.yahoo.com上下载,由于yahoo已经不再提供免费下载,所以要通过yfinance库获取,具体方法在文章结尾。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
四、数据探索#
us_economic_data = pd.read_csv('us_economic_data.csv')
us_economic_data.head()
| DATE | SP500 | PERMIT | INDPRO | FEDFUNDS | PSAVERT | CURRCIR | MPRIME | BUSLOANS | INTDSRUSM193N | DAUTOSAAR | CPIAUCSL | UNEMPLOY | PMSAVE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1985-01-01 | 179.630005 | 1660.0 | 54.7203 | 8.35 | 10.3 | 180.656 | 10.61 | 472.9593 | 8.00 | 8.244 | 105.7 | 8423 | 312.2 |
| 1 | 1985-02-01 | 181.179993 | 1662.0 | 54.9100 | 8.50 | 9.1 | 178.242 | 10.50 | 475.6222 | 8.00 | 8.308 | 106.3 | 8321 | 273.6 |
| 2 | 1985-03-01 | 180.660004 | 1727.0 | 54.9841 | 8.58 | 8.7 | 179.037 | 10.50 | 480.2038 | 8.00 | 8.380 | 106.8 | 8339 | 262.2 |
| 3 | 1985-04-01 | 179.830002 | 1664.0 | 54.8853 | 8.27 | 9.9 | 180.854 | 10.50 | 478.9746 | 8.00 | 8.474 | 107.0 | 8395 | 304.7 |
| 4 | 1985-05-01 | 189.550003 | 1709.0 | 54.9520 | 7.97 | 11.1 | 182.460 | 10.31 | 480.7533 | 7.81 | 8.227 | 107.2 | 8302 | 349.5 |
# Changing the column name and then setting the date as an index od the dataframe
df = us_economic_data
df['DATE'] = pd.to_datetime(df['DATE'])
df = df.set_index('DATE')
df.head()
| SP500 | PERMIT | INDPRO | FEDFUNDS | PSAVERT | CURRCIR | MPRIME | BUSLOANS | INTDSRUSM193N | DAUTOSAAR | CPIAUCSL | UNEMPLOY | PMSAVE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DATE | |||||||||||||
| 1985-01-01 | 179.630005 | 1660.0 | 54.7203 | 8.35 | 10.3 | 180.656 | 10.61 | 472.9593 | 8.00 | 8.244 | 105.7 | 8423 | 312.2 |
| 1985-02-01 | 181.179993 | 1662.0 | 54.9100 | 8.50 | 9.1 | 178.242 | 10.50 | 475.6222 | 8.00 | 8.308 | 106.3 | 8321 | 273.6 |
| 1985-03-01 | 180.660004 | 1727.0 | 54.9841 | 8.58 | 8.7 | 179.037 | 10.50 | 480.2038 | 8.00 | 8.380 | 106.8 | 8339 | 262.2 |
| 1985-04-01 | 179.830002 | 1664.0 | 54.8853 | 8.27 | 9.9 | 180.854 | 10.50 | 478.9746 | 8.00 | 8.474 | 107.0 | 8395 | 304.7 |
| 1985-05-01 | 189.550003 | 1709.0 | 54.9520 | 7.97 | 11.1 | 182.460 | 10.31 | 480.7533 | 7.81 | 8.227 | 107.2 | 8302 | 349.5 |
我们执行了Augmented Dickey-Fuller来确定SP500指数收盘价是否具有平稳性。之后我们对收盘价和每个自变量(经济指标)之间的数据进行可视化,以确定变量(经济指标)之间是否存在线性关系,从而仅选择其具有那些具有线性关系的变量用作建模。
其次,我们需要使用VIF测试检查自变量(经济指标)之间是否相互关联。最后,由于指标是在不同的统计范围上测量的,因此使用z score标准对数据进行了归一化,以产生准确可靠的模式。
def tsplot(y, figsize=(12, 7), syle='bmh'):
if not isinstance(y, pd.Series):
y = pd.Series(y)
with plt.style.context(style='bmh'):
fig = plt.figure(figsize=figsize)
layout = (2,1)
ts_ax = plt.subplot2grid(layout, (0,0), colspan=2)
y.plot(ax=ts_ax)
p_value = sm.tsa.stattools.adfuller(y)[1]
ts_ax.set_title('Time Series Analysis Plots\n Dickey-Fuller: p={0:.5f}'.format(p_value))
plt.tight_layout()
tsplot(df['SP500'])
data_diff = df['SP500'] - df['SP500'].shift(1)
tsplot(data_diff[1:])
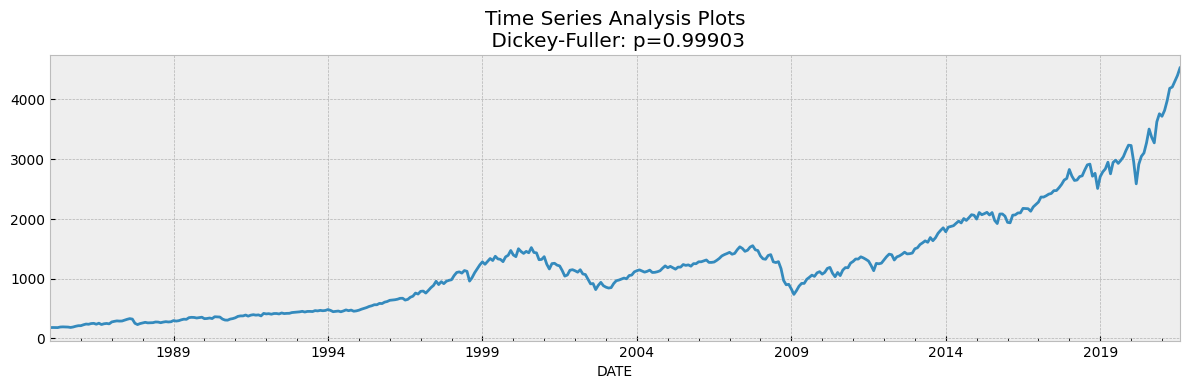
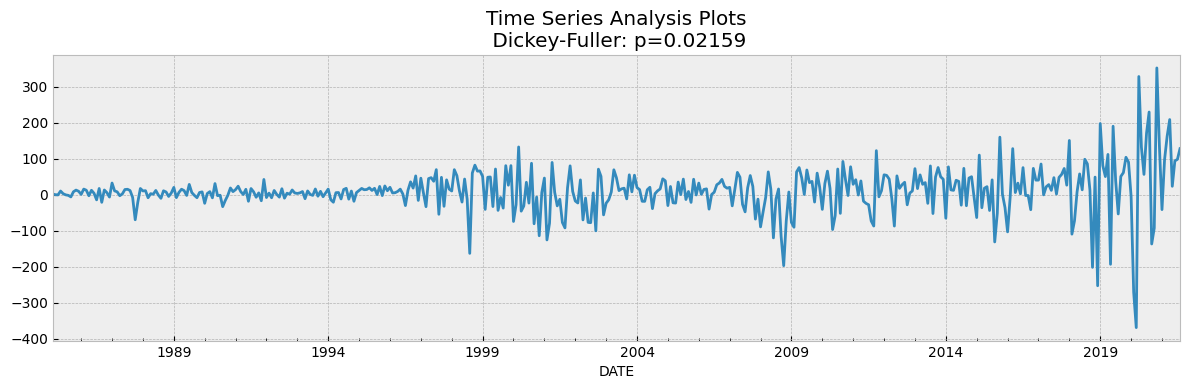
如果我们在Dickey Fuller Test的假设中取5%作为置信水平,我们可以看到值远大于0.05,因此可以判断SP500是不具备平稳性的。
为了使数据保持平稳,有必要创建一个新的因变量,该因变量是根据当前每月价格减去上个月的价格计算得出的。在这种情况下,重新计算前面提到的测试,并且发现数据是平稳的,因为p-value显示为0。
下一步是找出自变量是否彼此不相关。为此选择了 VIF(Variance Inflating factor, 方差膨胀因子)测试。方差膨胀因子 (VIF) 用于检验回归模型中是否存在多重共线性。
df.columns
Index(['SP500', 'PERMIT', 'INDPRO', 'FEDFUNDS', 'PSAVERT', 'CURRCIR', 'MPRIME',
'BUSLOANS', 'INTDSRUSM193N', 'DAUTOSAAR', 'CPIAUCSL', 'UNEMPLOY',
'PMSAVE'],
dtype='object')
# the independent variables set
X = df[['INTDSRUSM193N', 'BUSLOANS', 'MPRIME', 'FEDFUNDS', 'CURRCIR',
'PSAVERT', 'PMSAVE', 'DAUTOSAAR', 'UNEMPLOY', 'INDPRO', 'PERMIT',
'CPIAUCSL']]
# VIF dataframe
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
# calculating VIF for each feature
vif_data["VIF"] = [variance_inflation_factor(X.values, i)
for i in range(len(X.columns))]
print(vif_data)
feature VIF
0 INTDSRUSM193N 97.796219
1 BUSLOANS 182.967472
2 MPRIME 694.827208
3 FEDFUNDS 327.213964
4 CURRCIR 365.219235
5 PSAVERT 91.198794
6 PMSAVE 40.048740
7 DAUTOSAAR 63.977266
8 UNEMPLOY 62.133967
9 INDPRO 1337.341806
10 PERMIT 37.411240
11 CPIAUCSL 3058.034391
从上述表中可以看出,每个变量的 VIF 测试值远高于 10。在这种情况下,具有最高 VIF 值的指标将被删除,并重新计算整个集合。只要值小于 10 的所有变量都保留下来。
# the independent variables set
X = df[[ 'FEDFUNDS', 'CURRCIR','PSAVERT', 'PERMIT',]]
# VIF dataframe
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
# calculating VIF for each feature
vif_data["VIF"] = [variance_inflation_factor(X.values, i)
for i in range(len(X.columns))]
print(vif_data)
feature VIF
0 FEDFUNDS 6.149062
1 CURRCIR 7.253224
2 PSAVERT 7.123685
3 PERMIT 10.382944
我们发现其中 11 个经济指标不符合线性回归规则。
我们这阶段最后一步就是将这 3 个指标与SP500价格指数整合在一起,并根据z score标准对其进行标准化。
df_new = df[['SP500','FEDFUNDS','CURRCIR','PSAVERT','PERMIT']]
df_z_scaled = df_new.copy()
# apply normalization techniques
for column in df_z_scaled.columns:
df_z_scaled[column] = (df_z_scaled[column] -
df_z_scaled[column].mean()) / df_z_scaled[column].std()
# view normalized data
df_z_scaled.head()
| SP500 | FEDFUNDS | CURRCIR | PSAVERT | PERMIT | |
|---|---|---|---|---|---|
| DATE | |||||
| 1985-01-01 | -1.207185 | 1.749872 | -1.190784 | 1.118462 | 0.751727 |
| 1985-02-01 | -1.205417 | 1.803265 | -1.195481 | 0.702642 | 0.756793 |
| 1985-03-01 | -1.206010 | 1.831741 | -1.193934 | 0.564035 | 0.921442 |
| 1985-04-01 | -1.206957 | 1.721396 | -1.190398 | 0.979855 | 0.761859 |
| 1985-05-01 | -1.195873 | 1.614611 | -1.187274 | 1.395675 | 0.875847 |
五、建模#
现在,让我们继续在数据集上构建和评估机器学习模型。我们将首先为模型创建 features 和 labels,并将它们拆分为训练和测试示例。测试大小已保留为总数据集大小的 20%。
features = df_z_scaled.drop(columns = ['SP500'], axis = 1)
labels = df_z_scaled[['SP500']]
X_train, X_test, y_train, y_test = train_test_split(features, labels, test_size = 0.2, random_state = 0)
print(f"Shape of training data: {X_train.shape}")
print(f"Shape of the training target data: {y_train.shape}")
print(f"Shape of test data: {X_test.shape}")
print(f"Shape of the test target data: {y_test.shape}")
Shape of training data: (352, 4)
Shape of the training target data: (352, 1)
Shape of test data: (88, 4)
Shape of the test target data: (88, 1)
(1)Linear Regression#
regr = LinearRegression()
regr.fit(X_train, y_train)
print(regr.score(X_test, y_test))
0.9543343215374887
coefficients = pd.concat([pd.DataFrame(X.columns),pd.DataFrame(np.transpose(regr.coef_))], axis = 1)
coefficients
| 0 | 0 | |
|---|---|---|
| 0 | FEDFUNDS | 0.182386 |
| 1 | CURRCIR | 1.119148 |
| 2 | PSAVERT | -0.027447 |
| 3 | PERMIT | 0.118363 |
CURRCIR (Currency in Circulation)具有最高的系数,这意味着对模型的影响最大。
在模型适合我们的训练数据后,我们可以继续预测我们的测试集,以评估模型性能。让我们将预测存储在predicted中。
评估指标:
决定系数 (R^2)。这是数据中模型置信度的最重要指标,在回归模型的所有描述中都是必需的。
均方误差 (MSE)。此值测量实际值和预测值之间的均方根误差。
y_pred = regr.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print("MSE: ", mse)
print("RMSE: ", mse*(1/2.0))
r2 = r2_score(y_test, y_pred)
print('r2 score for Random Forest model is', r2)
MSE: 0.048140955259271416
RMSE: 0.024070477629635708
r2 score for Random Forest model is 0.9543343215374887
(2)RandomForest Regression#
下面使用了随机森林回归的方法,因为Random forest regression 考虑了多种预测结果,所以基于随机森林的预测更准确、算法更稳定。
rfr = RandomForestRegressor()
rfr.fit(X_train, y_train)
score = rfr.score(X_train, y_train)
print("R-squared:", score)
R-squared:
0.9988459424617248
ypred = rfr.predict(X_test)
mse = mean_squared_error(y_test, ypred)
print("MSE: ", mse)
print("RMSE: ", mse*(1/2.0))
r2 = r2_score(y_test, ypred)
print('r2 score for Random Forest model is', r2)
MSE: 0.005693238991363889
RMSE: 0.0028466194956819446
r2 score for Random Forest model is 0.9945994918507608
plt.figure(figsize=(5,5))
plt.scatter(y_test['SP500'].values, ypred, c='crimson')
p1 = max(max(ypred), max(y_test['SP500'].values))
p2 = min(min(ypred), min(y_test['SP500'].values))
plt.plot([p1, p2], [p1, p2], 'b-')
plt.xlabel('True Values', fontsize=15)
plt.ylabel('Predictions', fontsize=15)
plt.axis('equal')
plt.show()
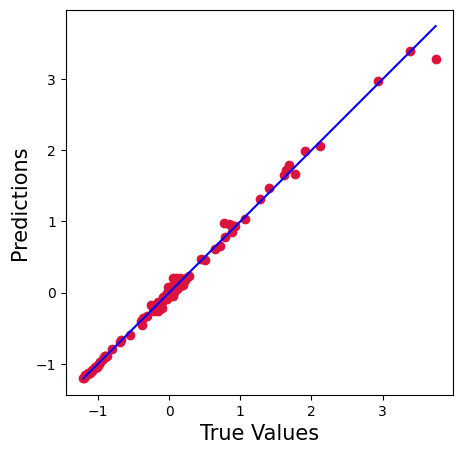
根据两种回归方法得出的 R2 和 MSE/RMSE,随机森林模型在这例子中显然较优, 其统计线性回归模型中提高了 6%,错误率降低了 20 倍。
【数据获取过程】#
from pandas_datareader import data as pdr
import yfinance as yf
yf.pdr_override()
# download dataframe
data = pdr.get_data_yahoo("^GSPC", start="1985-01-01", end="2022-06-01", interval = "1mo")
data = data.rename(columns={'Close':'SP500'})
data.index.names=['DATE']
data = data[['SP500']]
data.to_csv('../data/sp500.csv')
import pandas as pd
import os
import glob
PATH_DIR = '../data'
file_paths = sorted(glob.iglob(PATH_DIR + '/*'), key=os.path.getmtime)
df_merge=pd.read_csv(PATH_DIR+'/sp500.csv')
df_merge = df_merge.set_index('DATE')
for fp in file_paths:
if 'sp500' not in fp:
df = pd.read_csv(fp)
df = df.set_index('DATE')
df_merge = df_merge.join(df, how='inner')
df_merge.to_csv('../us_economic_data.csv')

